RISCO SISTEMÁTICO DE LONGEVIDADE EM PLANOS PREVIDENCIÁRIOS

SYSTEMATIC LONGEVITY RISK IN SOCIAL SECURITY PLANS 

Mainara de Paula Simões Cardoso [1]

Alane Siqueira Rocha [2] 

RESUMO

O risco de longevidade está presente na estrutura do sistema previdenciário brasileiro e pode ser definido como a probabilidade de os participantes de planos de previdência sobreviverem além do esperado. O objetivo geral deste trabalho é mensurar o impacto do risco de longevidade na solvência de planos de previdência com pagamento de benefícios vitalícios. Foi desenvolvido um modelo na linguagem Python que utilizou o processo de Simulação de Monte Carlo para desvendar as distribuições de probabilidades das provisões matemáticas para amostras com diferentes tamanhos. A partir da análise dos resultados, concluiu-se que o coeficiente de variação e a taxa de carregamento de contingência diminuem, tendendo a zero, à medida que o tamanho da população aumenta. Entretanto, a inclusão do risco sistemático de longevidade gera um cenário distinto, no qual a redução do carregamento de contingência atinge um limiar, ocasionando, portanto, reduções mínimas entre grupos de 5.000 a 50.000 segurados.

Palavras-chave: Previdência; Longevidade; Risco Sistemático; Solvência; Simulação de Monte Carlo.

ABSTRACT

The phenomenon of longevity risk permeates the structural framework of the Brazilian pension system and is defined as the probability of pension plan participants surpassing their projected life expectancies. This research paper is primarily concerned with quantifying the influence of longevity risk on the financial stability of pension plans offering lifelong benefits. A model was developed using the Python programming language, employing the Monte Carlo Simulation method to unveil the probability distributions of mathematical provisions across various sample sizes. A comprehensive examination of the empirical findings has led to the deduction that both the coefficient of variation and the contingency loading rate exhibit a consistent decreasing trend, asymptotically approaching zero as the size of the beneficiary population increases. Nevertheless, the inclusion of systematic longevity risk gives rise to an alternative scenario, wherein risk reduction reaches a threshold, resulting in minimal reductions among groups comprising 5,000 to 50,000 policyholders.

Keywords: Pension Plans; Longevity Risk; Systematic Risk; Solvency Analysis; Monte Carlo Simulation.

1. Introdução

Os planos de previdência possuem grande importância para a sociedade, pois têm como principal objetivo garantir uma renda para os trabalhadores e seus dependentes quando ocorre a perda da capacidade de trabalho, seja por invalidez, envelhecimento, morte do indivíduo, entre outras razões.

Em relação à duração dos benefícios de renda dos planos de previdência, os pagamentos podem ser temporários, normalmente estruturados na modalidade de contribuição definida, ou vitalícios, que estão sujeitos ao risco de longevidade. Esse risco pode ser definido como a probabilidade de os participantes de planos de previdência sobreviverem além do esperado, exaurindo suas reservas (RIBEIRO; CHARIGLIONE; SILVA, 2020).

O aumento da longevidade é considerado um indicador de desenvolvimento dos países e vem se consolidando ao redor do mundo. Entretanto, para os planos de previdência com benefícios vitalícios, esse aumento do tempo médio de vida se torna uma preocupação relevante, considerando a promessa de pagamento de benefícios vitalícios. Esse aumento da sobrevida dos participantes dos planos previdenciários deve ser incorporado nos cálculos atuariais de maneira que não subestime ou superestime suas provisões matemáticas.

O risco de longevidade está presente na estrutura do sistema previdenciário brasileiro. No âmbito da previdência social, os planos previdenciários brasileiros com pagamento de benefícios vitalícios estão presentes na previdência dos servidores públicos, administrada pelo Regime Próprio de Previdência Social (RPPS), e na previdência dos funcionários do setor privado, administrada pelo Regime Geral de Previdência Social (RGPS).

No contexto da previdência complementar, tais planos de benefícios vitalícios também estão presentes e são oferecidos nos planos administrados pelas Entidades Abertas de Previdência Complementar (EAPC), os quais são acessíveis a qualquer pessoa física, assim como nos planos geridos pelas Entidades Fechadas de Previdência Complementar (EFPC). Esses últimos são restritos aos funcionários de empresas ou aos associados de categorias ou setores específicos. 

O risco de longevidade, de acordo com Hári et al. (2008), pode ser dividido em duas categorias: risco de microlongevidade, que diz respeito à aleatoriedade do momento da morte quando as probabilidades de sobrevivência são conhecidas, e macrolongevidade, que envolve a incerteza em relação às probabilidades de sobrevivência futuras. Aro (2012) adota nomenclaturas alternativas para esses riscos, denominando-os, respectivamente, como risco não sistemático e sistemático. 

Bravo (2007) destaca a possibilidade de mitigar o risco de aleatoriedade ao aumentar o número de segurados em um plano de benefícios previdenciais. No entanto, o risco sistemático persiste, mesmo com o aumento do tamanho do grupo segurado. É importante salientar que, na análise de Bravo (2007), as mortalidades dos participantes nesses planos previdenciários são consideradas independentes entre si, resultando em correlação nula. 

Portanto, para obter uma gestão mais eficaz do risco atuarial em um plano de previdência, é essencial que ambos os componentes do risco de longevidade – risco de aleatoriedade (não sistemático) e risco sistemático – sejam devidamente mensurados. Nesse contexto, surge a relevante questão de como esses componentes podem ser avaliados no contexto do sistema previdenciário brasileiro. 

Dessa forma, o objetivo geral desta pesquisa é mensurar o impacto do risco de longevidade na solvência de planos de previdência que oferecem benefícios vitalícios. Os objetivos específicos incluem o desenvolvimento de um modelo estocástico de cálculo atuarial e a avaliação do risco de aleatoriedade e do risco sistemático em planos de benefícios vitalícios, considerando diferentes tamanhos de grupos populacionais. Embora na prática atuarial o resultado de modelos determinísticos seja comumente utilizado para contabilizar as obrigações atuariais, o modelo estocástico pode ser adotado, por exemplo, para dimensionar potenciais fundos de oscilação de risco. 

Nesse sentido, foi elaborado um modelo computacional em linguagem Python que empregou o método da Simulação de Monte Carlo para elucidar as distribuições de probabilidade das provisões matemáticas em distintos grupos, considerando diferentes tamanhos amostrais. Esse procedimento foi realizado em dois cenários distintos: um levando em consideração exclusivamente o risco de aleatoriedade e outro que também incorporou o efeito do risco sistemático. Os grupos de diferentes tamanhos foram extraídos da base de dados fornecida pelo Ministério do Planejamento, Orçamento e Gestão (MPOG) no contexto da reforma da previdência ocorrida em 2019. Para o cálculo atuarial, foi utilizado um plano de benefícios previdenciais hipotético.

2. Revisão de literatura 

Rodrigues (2008) enfatiza que os riscos atuariais em Fundos de Pensão devem ser compreendidos como eventos provenientes de fatores que introduzem volatilidade nos resultados necessários para a solvência dos Planos de Benefícios. No cálculo atuarial de planos de pensão, os dois principais riscos são aqueles relacionados às premissas do mercado financeiro e às premissas biométricas. De acordo com Rodrigues (2008), o risco biométrico é definido como a possibilidade de premissas biométricas, como mortalidade e invalidez, não se concretizarem conforme o previsto.

Este estudo se concentrará exclusivamente no tratamento do risco de longevidade, classificado como um risco biométrico, conforme definido no Guia Previc Melhores Práticas Atuariais (2022). Esse tipo de risco diz respeito à potencial ampliação da expectativa de vida dos participantes e beneficiários dos planos de benefícios com o passar do tempo.

Segundo Rodrigues (2008), o caráter vitalício dos benefícios proporciona uma conceituação diferenciada para a tomada de riscos pela extensão do período de sua responsabilidade. A acumulação da reserva desses planos compreende a fase que vai da adesão ao plano até a aposentadoria (ou pela geração de pensão por morte de participante ativo) e deve ser suficiente para pagar de forma vitalícia, até o falecimento do participante ou de seu beneficiário, o benefício contratado.

Nos estudos conduzidos por Hári et al. (2008), Aro (2012) e Bravo (2007), a análise do risco de longevidade é desdobrada em dois componentes: o primeiro refere-se à incerteza em torno do momento da morte, considerando que as probabilidades de sobrevivência são conhecidas, o segundo componente diz respeito à incerteza acerca das probabilidades de sobrevivência futuras. Esses dois componentes são denominados por Bravo (2007) como risco de aleatoriedade (risco não sistemático) e risco sistemático, respectivamente.

Aro (2012) esclarece, ainda, que o risco de longevidade sistemático não é diversificável e não depende do tamanho da população. Já o risco de longevidade não sistemático diminui à medida que o tamanho da população aumenta. Nessa linha, Bravo (2007) esclarece que a incerteza em torno da longevidade humana pode decompor-se em diferentes fontes de risco, como por exemplo, as flutuações aleatórias nas taxas de mortalidade (risco de aleatoriedade) e os desvios sistemáticos (risco sistemático).

Bravo (2007) pontua que o risco de aleatoriedade, também conhecido de risco não sistemático, pode ser reduzido à medida que o tamanho do grupo segurado aumenta, de acordo com o princípio da lei dos grandes números. Nesse sentido, quanto maior for a população, menor será a probabilidade de ocorrerem flutuações aleatórias nas taxas de mortalidade, uma vez que essas flutuações se tornam menos significativas com o aumento do número de segurados. Por outro lado, no que diz respeito ao risco sistemático, não é possível eliminar esse risco através do aumento do número de segurados. Pelo contrário, seu impacto financeiro se intensifica à medida que o número de segurados cresce, uma vez que os desvios afetam uniformemente todos os indivíduos do grupo.

Dessa forma, de acordo com Bravo (2007), o risco de aleatoriedade está diretamente ligado à variação esperada no número de óbitos em relação à média e apresenta uma relação inversa com o tamanho da população. Por outro lado, o risco sistemático está relacionado a alterações na expectativa de sobrevivência do grupo como um todo, que podem ser provocadas por fatores que afetam todos os indivíduos simultaneamente, como avanços na área da medicina e inovações tecnológicas em saúde.

No contexto brasileiro, há alguns estudos que se dedicam a analisar o risco de aleatoriedade em planos previdenciários. Cardoso et al. (2006) realizaram simulações, utilizando dados hipotéticos, com objetivo de mensurar a variabilidade das obrigações de uma Entidade Fechada de Previdência Complementar (EFPC) e constataram que as taxas de carregamento das obrigações previdenciárias são decrescentes com o aumento do grupo. Dias e dos Santos (2009) mensuraram os passivos atuariais de fundos previdenciários de forma estocástica através da Simulação de Monte Carlo e analisaram a sensibilidade do passivo em relação à alteração das tábuas de mortalidade.

No estudo conduzido por Corrêa, Queiroz e Ribeiro (2014), foi examinado o efeito da variação nos eventos demográficos na solvência dos Regimes Próprios de Previdência Social (RPPS) municipais. Os resultados da pesquisa apontaram para uma correlação entre o tamanho da população e o risco de solvência dos planos previdenciários. Constatou-se que em municípios com populações menores, o risco relacionado aos fatores demográficos tende a ser mais acentuado. Além disso, observou-se que em situações de maior rentabilidade, esse risco também se amplifica.

Contudo, as pesquisas conduzidas por Cardoso et al. (2006), Corrêa, Queiroz e Ribeiro (2014) e Dias e dos Santos (2009) não incluíram uma análise da avaliação do risco sistêmico decorrente de uma alteração simultânea na longevidade de todos os membros do grupo.

Hári et al. (2008) e Aro (2021) subdividem o risco relacionado à longevidade em diferentes portfólios de renda e investigaram tanto o impacto do risco sistemático de longevidade quanto do risco não sistemático de longevidade. Esses estudos analisam como a diversificação pode afetar o risco não sistemático, diminuindo sua influência à medida que a população aumenta. Por outro lado, é importante notar que o risco de longevidade sistemático não pode ser mitigado por meio da diversificação e não está vinculado ao tamanho da população.

Oliveri e Pitacco (2001) conduziram uma análise do impacto do risco sistemático na solvência de planos de benefícios para cuidados de longa duração (CLD), que se referem aos serviços de cuidado contínuo prestados a idosos dependentes, necessitando de auxílio para realizar atividades diárias, conforme definido por Rocha (2015). Os autores exploraram as três principais teorias que descrevem a evolução da morbidade. Os cenários delineados por essas teorias têm implicações substancialmente distintas para as seguradoras, gerando um elevado grau de incerteza em relação à evolução das condições de saúde, o que, por sua vez, requer a inclusão dessas variabilidades no modelo atuarial empregado na avaliação dos benefícios. Enquanto os métodos atuariais tradicionais para projeções demográficas fazem extrapolações de tendências com base em dados observados, a pesquisa realizada por Oliveri e Pitacco (2001) adotou uma abordagem diferente, na qual foram delineados possíveis cenários futuros relativos à duração esperada em estados de saúde plena e estados de incapacidade.

No estudo conduzido por Oliveri e Pitacco (2001), a margem de solvência requerida apresentou uma diminuição à medida que o número de segurados aumentou no cenário determinístico estabelecido. No entanto, ao incorporar as diferentes perspectivas sobre a evolução da morbidade, observou-se um aumento na margem de solvência necessária. O valor relativo da margem de solvência requerida teve uma leve redução com o aumento do tamanho do grupo segurado. No entanto, ao contrário do cenário determinístico, pareceu haver um valor mínimo positivo da margem de solvência requerida, independentemente do tamanho do grupo, devido à presença do risco sistemático.

Neste estudo, além de investigar a conexão entre o tamanho da população e o risco associado à aleatoriedade na mortalidade, será quantificado o efeito do risco sistemático de longevidade em grupos de diferentes dimensões em planos de previdência, de maneira semelhante à avaliação realizada por Oliveri e Pitacco (2001) em relação a planos de cuidados de longa duração.

 3. Dados e método 

Com objetivo de analisar o impacto da variabilidade e dos desvios sistêmicos de mortalidade na solvência de planos de previdência, em diferentes tamanhos de população, foram calculadas as distribuições de probabilidades das provisões matemáticas com vários níveis de solvência para grupos com diferentes tamanhos. 

Para esse fim, foram extraídas sete amostras com tamanhos variados a partir da base de ativos, aposentados e pensionistas disponibilizada pelo Ministério do Planejamento, com data-base referente a outubro de 2018. Essa base foi disponibilizada pelo governo federal no contexto das discussões sobre a Reforma da Previdência, que foi aprovada pelo Congresso Nacional em 12 de novembro de 2019. As gerações das amostras, com perfis semelhantes à base original, foram realizadas por meio da função de estratificação sklearn.model_selection.train_test_split disponibilizada no pacote scikit-learn da linguagem de programação Python.

Essas subamostras, com composições semelhantes à base original, continham populações de 50, 100, 500, 1.000, 5.000, 10.000 e 50.000 indivíduos, respectivamente. As amostras foram estratificadas de forma a manter aproximadamente a mesma proporção de ativos (45,9%), aposentados (34,1%) e pensionistas (19,9%) em relação à base original. Além disso, foram preservadas as proporções semelhantes das variáveis, como sexo, idade, salário dos ativos, cargo (professor ou não) dos ativos, benefício de aposentadoria, estado de validez dos aposentados, benefício de pensão e duração da pensão.

 3.1 Plano de benefícios

O rol de benefícios considerado para o cálculo das provisões matemáticas abrange aposentadoria programada, aposentadoria por invalidez e pensão por morte do participante ativo normal ou do participante aposentado. No Quadro 1, são apresentadas as especificações dos benefícios disponibilizados pelo plano hipotético, incluindo suas modalidades, tipos (programado ou não) e níveis correspondentes. 

Quadro 1 - Características dos benefícios

Fonte: Elaboração própria.

O critério de elegibilidade para os participantes receberem o benefício de renda de aposentadoria programada é atingir a idade mínima de 65 anos para os homens e de 62 anos para as mulheres. 

Quanto às contribuições utilizadas para o cálculo, foi estabelecido um valor equivalente a 28% do salário do servidor, dos quais 14% são suportados pelo servidor em atividade e outros 14% pelo patrocinador. Além disso, os aposentados que recebem benefícios que excedem o limite do Regime Geral de Previdência Social (RGPS) devem contribuir com 14% sobre o valor excedente do benefício.

3.2 Premissas atuariais utilizadas

De acordo com o Guia Previc Melhores Práticas Atuariais (2022), as hipóteses atuariais constituem os fundamentos técnicos da avaliação atuarial. O equilíbrio dos planos previdenciários e os riscos que o envolvem passam, em grande medida, pelas premissas atuariais adotadas e pela metodologia de cálculo empregada (CORRÊA, 2014). Este estudo, no entanto, não tem o intuito de verificar a adequação das premissas para um determinado grupo.

Uma vez que a base de dados utilizada neste trabalho foi oriunda dos servidores civis do Governo Federal, adotou-se hipóteses utilizadas na avaliação atuarial do encerramento do exercício de 2021 do Plano de Benefícios ExecPrev. Plano de previdência complementar destinado aos servidores públicos federais do poder Executivo, administrado pela Funpresp-Exe e cuja população dos segurados é um subgrupo dos servidores ativos civis que consta na base utilizada para o cálculo deste estudo. Além disso, em alguns casos, foram adotadas as premissas utilizadas na avaliação atuarial do RPPS da União. As premissas atuariais foram classificadas em duas categorias: econômicas e demográficas, as quais estão detalhadas no Quadro 2. 

Quadro 2 – Premissas Atuariais

Fonte: Elaboração própria.

 3.3 Modelo atuarial

Segundo Olivieri e Pitacco (2001), a probabilidade de eventos como mortalidade e invalidez depende das hipóteses adotadas para determinar esses eventos futuros em um determinado cenário assumido. Para qualquer cenário, uma estrutura probabilística condicional pode ser construída. Os autores explicam que de acordo com essa abordagem, chamada de teste de cenários, diferentes cenários razoáveis são considerados e os cálculos relevantes são realizados. Dessa forma, o teste de cenários engloba o risco de flutuações e fornece uma informação aproximada sobre os desvios sistêmicos, normalmente por meio de faixas para alguns resultados, que podem ser de valores esperados, variâncias, percentis ou outros.

De maneira semelhante à avaliação realizada por Oliveri e Pitacco (2001), neste estudo, além de investigar a conexão entre o tamanho da população e o risco associado à aleatoriedade na mortalidade, será quantificado o efeito do risco sistemático de longevidade em grupos de diferentes dimensões em planos de previdência. Para esse fim, foram calculadas as provisões matemáticas através de um programa desenvolvido em Python, com o intuito de comparar a taxa de carregamento de contingência com distintas probabilidades de solvência para os grupos. Assim, por meio do processo de Simulação de Monte Carlo, foram realizadas corridas com 5.000 iterações para cada indivíduo, desvendando as distribuições de probabilidades da variável valor agregado das provisões matemáticas para cada um dos sete grupos populacionais formados.

Paralelamente, foram conduzidas simulações adicionais nas quais as premissas e os tamanhos dos grupos foram mantidos constantes, contudo, a projeção de mortalidade passou a incorporar o impacto do risco sistemático. Nesse contexto, para cada iteração, a escolha da tabela a ser empregada baseou-se na probabilidade atribuída a três cenários de mortalidade distintos com a mesma probabilidade de ocorrência: ausência de agravo, com agravo de 25% e com desagravo de 25%.

A partir da comparação dos resultados encontrados com as simulações, realizou-se uma análise da influência do tamanho do grupo no nível de carregamento de contingência para o plano de previdência, tanto com quanto sem a inclusão do risco sistemático.

 4. Resultados e discussões

Para evidenciar o risco de aleatoriedade e o risco sistemático na longevidade, foram comparados os coeficientes de variação das provisões matemáticas e as taxas de carregamento de contingência para determinada probabilidade de solvência para os grupos com diferentes tamanhos.

Para o risco aleatório de longevidade, são apresentadas, na Tabela 1, três medidas da variável provisão matemática: a sua esperança, o seu desvio padrão e seu coeficiente de variação, que mede a relação entre o desvio padrão e a média e é “uma medida útil para a comparação do grau de concentração em torno da média de séries distintas” (CARDOSO et al., 2006, p. 30).

Os resultados evidenciam que o coeficiente de variação reduz à medida que o tamanho do grupo aumenta, passando de 7,0% no grupo de 50 segurados para 0,2% no grupo com 50.000 segurados. Esse efeito foi semelhante ao observado por Cardoso et al. (2006), que constataram que os coeficientes de variação das obrigações previdenciais são decrescentes com o aumento do tamanho do grupo.

Tabela 1 – Estatísticas das provisões matemáticas por tamanho do grupo, apenas com risco aleatório de longevidade

Fonte: Elaboração própria. 

Na Tabela 2, são apresentadas as mesmas três medidas da variável provisão matemática, mas, dessa vez, para o cenário com a inclusão do risco sistemático. Nesse cenário, evidencia-se que o coeficiente de variação, a esperança e o desvio-padrão aumentaram, quando comparados ao cenário sem o risco sistemático. Além disso, percebe-se que a redução do coeficiente de variação com aumento do tamanho do grupo é relativamente menor do que no cenário sem o risco sistemático.

Tabela 2 - Estatísticas das provisões matemáticas por tamanho do grupo, com risco aleatório e risco sistemático de longevidade

Fonte: Elaboração própria.

Outra forma de evidenciar o efeito do risco de aleatoriedade e do risco sistemático na longevidade é a comparação entre as taxas de carregamento de contingência sobre as provisões matemáticas. Na Tabela 3, observa-se que, nas simulações sem a inclusão do risco sistemático, as taxas de carregamento de contingência sobre as obrigações de um grupo diminuem com o aumento do tamanho do grupo. Nos grupos com 50 e 100 segurados, essas taxas são de 11,4% e 6,1%, respectivamente, para 95% de probabilidade de solvência; enquanto para o grupo de 50.000, essa taxa é de apenas 0,3%, próximo a zero, evidenciando o efeito da redução desse risco com a diversificação da população de segurados.

Cardoso et al. (2006) também observaram essa relação e pontuaram que essas taxas elevadas para os pequenos grupos dificultam a constituição de planos com poucos participantes. Além disso, os autores ressaltaram que grupos com pequeno número de participantes têm ainda uma dificuldade relativa às despesas administrativas, o que contribui adicionalmente para dificultar a implementação de planos de previdência para pequenos grupos.

Tabela 3 – Taxas de carregamento para 90%, 95% e 99% de probabilidade de solvência para cada tamanho do grupo, apenas com risco aleatório de longevidade

Fonte: Elaboração própria.

Na Tabela 4, pode-se examinar a análise das taxas de carregamento para diferentes subgrupos de segurados, excluindo também o impacto do risco sistêmico. Nesse contexto, nota-se, por exemplo, que as taxas calculadas para os subgrupos populacionais (ativos, aposentados e pensionistas) são superiores às taxas observadas para o conjunto total da população segurada. Uma possível explicação para esse fenômeno reside na correlação negativa entre os benefícios de risco e os benefícios programados, como discutido por Cardoso et al. (2006) em suas observações sobre essa relação.

Tabela 4 - Taxas de carregamento para 90%, 95% e 99% de probabilidade de solvência para cada tamanho do grupo, apenas com risco aleatório de longevidade

Ativos

Aposentados

Pensionistas

Fonte: Elaboração própria.

Na Tabela 5, foi calculada a taxa de carregamento de contingência levando em conta as provisões matemáticas que incorporaram o efeito do risco sistemático em seu cálculo. Quando o risco sistemático é considerado, as taxas de carregamento são superiores ao cenário que exclui o risco sistemático. Observa-se também uma redução nas taxas de carregamento à medida que o tamanho do grupo aumenta. No entanto, é importante destacar que esse cenário se diferencia, uma vez que a redução da taxa atinge um limiar, ocasionando, pequenas reduções entre grupos de 5.000 a 50.000 segurados.

Tabela 5 - Taxas de carregamento para 90%, 95% e 99% de probabilidade de solvência para cada tamanho do grupo, considerando todo o grupo e efeito do risco sistemático

Fonte: Elaboração própria.

Para um horizonte de cinco anos e uma solvência de 97,5%, Hári et al. (2008) estimaram esse carregamento limite, dependendo do tamanho do grupo de segurados, na ordem de grandeza de 7% a 8% sobre as provisões matemáticas. Analisando a solvência em produtos de cuidados de longa duração (CLD), Olivieri e Pitacco (2001) perceberam que, em decorrência do desvio sistêmico, parece haver um valor mínimo positivo da margem de solvência exigida, independentemente do tamanho do grupo de segurados. De maneira análoga, essa mesma dinâmica parece ocorrer em planos de previdência quando o risco sistemático é levado em consideração.

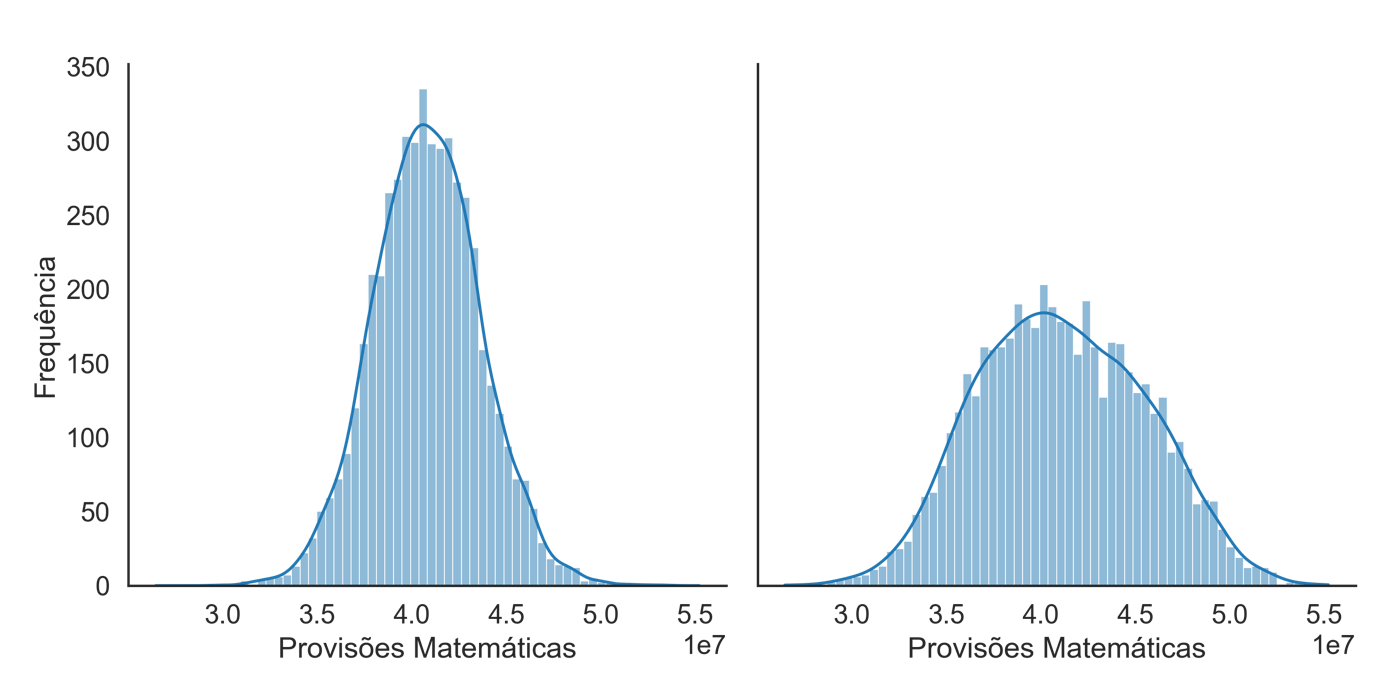
As Figuras 1 e 2 apresentam a distribuição do valor das provisões matemáticas dos grupos de 50 e 50.000 segurados, mostrando os cenários com e sem o risco sistemático. As distribuições são acompanhadas por curvas de suavização geradas pelo Método de Estimação por Kernel, uma abordagem não-paramétrica para estimar a Função Densidade de Probabilidade de uma variável aleatória, sendo esta visualização confeccionada por meio do pacote gráfico seaborn.

Figura 1  – Distribuição da Provisão Matemática para o grupo com 50 segurados   

 Fonte: Elaboração própria.

Figura 2 – Distribuição da Provisão Matemática para o grupo com 50.000 segurados        

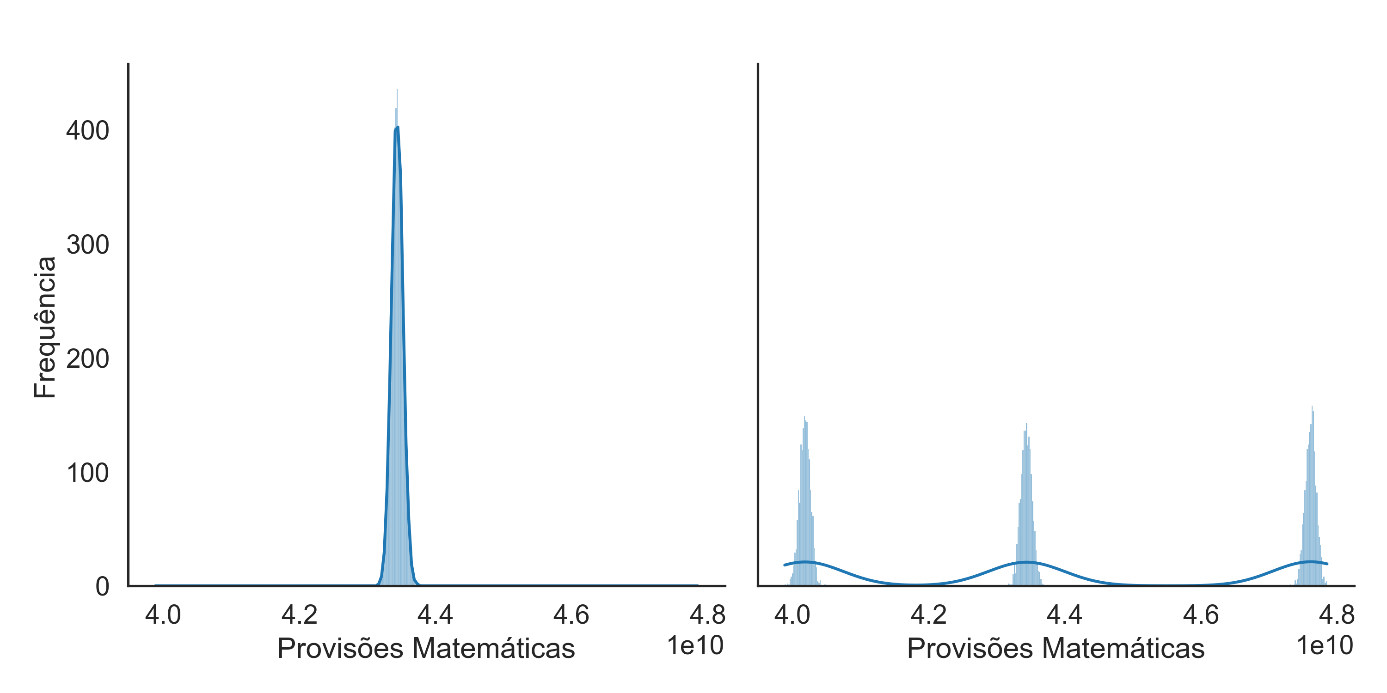
Fonte: Elaboração própria.

Ao analisar as distribuições apresentadas nas Figuras 1 e 2, ao levar em conta o risco sistemático, percebe-se que a distribuição para grandes grupos, tais como 50.000 segurados, não segue uma tendência normal (o teste Kolgomorov-Smirnov de normalidade resultou em um p-valor próximo a zero), apresentando, em vez disso, uma característica multimodal.

As Figuras 3 e 4 apresentam a variação nos pagamentos projetados para um grupo mais amplo, composto por 50.000 segurados, utilizando gráficos do tipo box-plot. Esses gráficos ilustram a variação nos pagamentos, levando em conta a presença ou ausência do risco sistemático. Ao comparar as distribuições nos dois cenários, percebe-se que a variação nos pagamentos ao longo do período projetado é significativamente menor quando o risco sistemático é excluído. Por outro lado, no cenário que inclui o risco sistemático, é evidente que persiste uma considerável variabilidade nos pagamentos.

Figura 3 – Fluxo de pagamentos projetados para o grupo com 50.000 segurados sem o risco sistemático

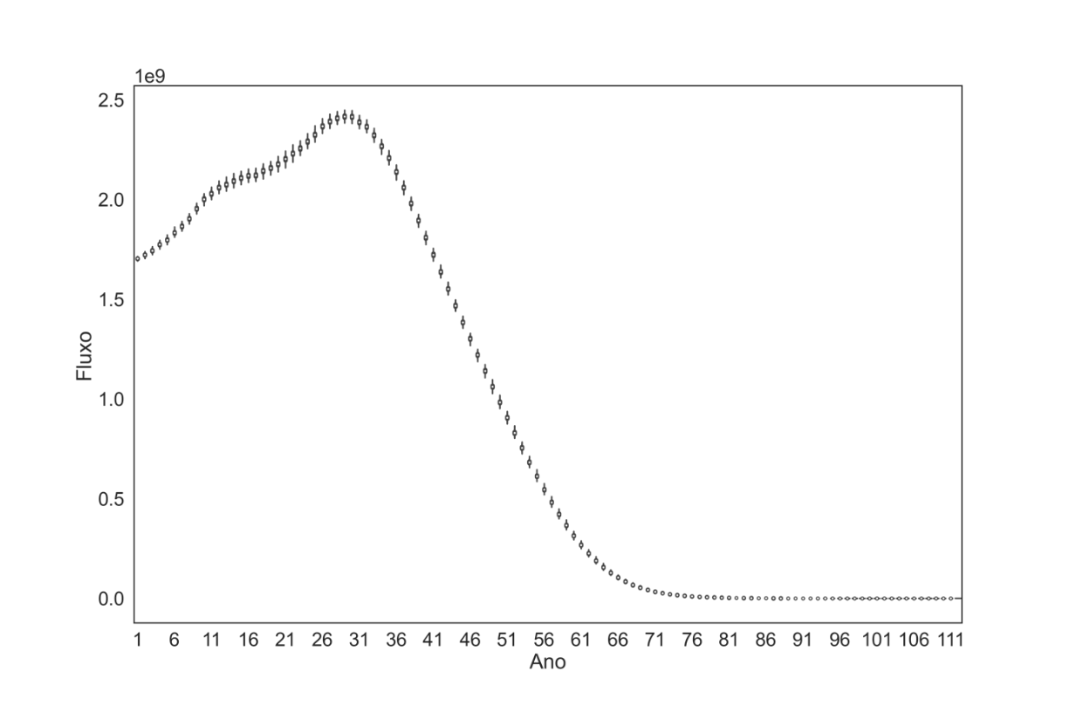
 Fonte: Elaboração própria

Figura 4 – Fluxo de pagamentos projetados para o grupo com 50.000 segurados com o risco sistemático

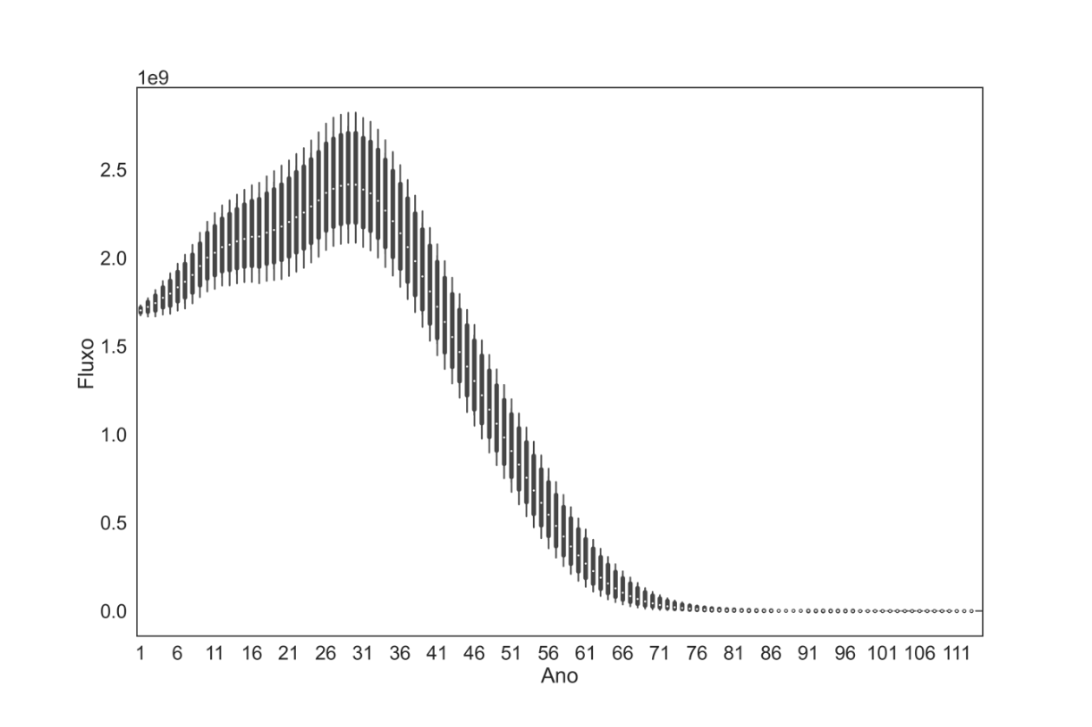
 Fonte: Elaboração própria

Assim, os resultados demonstraram que a inclusão do risco sistemático torna o risco de longevidade em planos que oferecem benefícios vitalícios relevante, mesmo quando o grupo é de grande porte. Uma das estratégias para gerenciar esse risco é compartilhá-lo com uma seguradora. Uma alternativa viável é a adoção de desenhos de planos de benefícios nos quais apenas uma parte reduzida esteja exposta ao risco de longevidade. Por exemplo, podem ser considerados desenhos de planos de previdência complementar estruturados na modalidade de contribuição definida.

5. Considerações finais

O propósito deste estudo consistiu em quantificar o impacto dos riscos de aleatoriedade e do risco sistemático de longevidade nas provisões matemáticas de planos de previdência que oferecem benefícios vitalícios, considerando diferentes tamanhos de população. Para isso, foi concebido um modelo de cálculo estocástico, implementado na linguagem de programação Python, fazendo uso do método de Simulação de Monte Carlo para elucidar as distribuições probabilísticas das provisões matemáticas em grupos de tamanhos variados. Foram delineados dois cenários: um considerando somente o risco de aleatoriedade e outro incorporando, adicionalmente, o risco sistemático.

A partir da análise dos resultados, pôde-se constatar que tanto o coeficiente de variação quanto a taxa de carregamento de contingência diminuem à medida que a dimensão populacional aumenta. Quando o risco de aleatoriedade é o único considerado, excluindo o risco sistemático, o coeficiente de variação passa de 7,0% no grupo com a menor amostra, composto por 50 segurados, para 0,2% quando calculado para o grupo de 50.000 segurados. A taxa de carregamento, com uma margem de solvência de 90%, reduz-se de 8,7% para 0,2% ao comparar os dois grupos.

 Quando introduzido o risco sistemático de longevidade, os achados indicaram que a redução do risco atinge um limite.  A comparação do coeficiente de variação entre os grupos de 50 e 50.000 segurados evidencia uma redução de 10,9% para 7,0%, aproximando-se do patamar alcançado pelo grupo de 5.000 segurados. Da mesma maneira, a taxa de carregamento, mantendo uma margem de solvência de 90%, também apresenta uma redução à medida que o tamanho do grupo diminui, caindo de 14,7% para 8,9%.

 Esses achados corroboram com os resultados previamente constatados por Cardoso et al. (2006), que indicaram que o risco de longevidade diminui à medida que o número de segurados no plano previdenciário aumenta. Contudo, dado que o risco sistemático persiste independentemente do tamanho do grupo, essa redução ocorre até que um limite seja atingido.

 Uma das estratégias para o gerenciamento deste risco consiste em compartilhá-lo com uma seguradora, que pode inclusive ressegurar parte dessa exposição. Entretanto, quando o risco é de natureza global, o mercado segurador pode enfrentar desafios consideráveis para assumir tais riscos. Uma alternativa viável é a adoção de desenhos de planos de benefícios em que apenas uma parcela reduzida esteja exposta ao risco de longevidade. Por exemplo, consideram-se desenhos de planos de previdência complementar estruturados na modalidade de contribuição definida durante a fase de acumulação e nos primeiros estágios da fase de concessão.

 Este estudo representa uma contribuição valiosa para a escassa literatura relacionada ao risco de longevidade em planos previdenciários, considerando a relevância do mercado de previdência para a população brasileira. No entanto, é importante notar que este estudo se concentrou exclusivamente na análise do risco de longevidade, excluindo outras fontes de risco. Portanto, sugere-se que investigações futuras incorporem o risco de mercado em planos de previdência com benefícios vitalícios. Além disso, a abordagem dos cenários de mortalidade e suas respectivas probabilidades não fez parte do escopo deste estudo, indicando a necessidade de pesquisas subsequentes que explorem essa dimensão.

Referências

ARO, H. Longevity 8: Systematic and non-systematic mortality risk in pension portfolios. 2012. Disponível em: http://math.aalto.fi/~haro/bin.pdf

BRASIL. Lei complementar n^o 109, de 29 de maio de 2001. Dispõe sobre o Regime de Previdência Complementar e dá outras providências. Brasília, DF: Casa Civil, 2001. Disponível em: http://www.planalto.gov.br/ccivil_03/LEIS/LCP/Lcp109.htm. Acesso em: 15 jul. 2022.

BRASIL. MINISTÉRIO DA ECONOMIA. PREVIC. Guia Previc de Melhores Práticas Atuariais para Entidades Fechadas de Previdência Complementar. Superintendência Nacional de Previdência Complementar, 2021. Disponível em: https://www.gov.br/economia/pt-br/orgaos/entidadesvinculadas/autarquias/previc/centrais-de-conteudo/publicacoes/guias-de-melhorespraticas/novo-guia-previc-melhores-atuariais.pdf/view. Acesso em: 22 jul. 2022.

BRASIL. MINISTÉRIO DA ECONOMIA. PREVIC. Resolução CNPC nº 41, 09 de junho de 2021. Disponível em: https://www.gov.br/trabalho-e-previdencia/pt-br/acesso-a-informacao/participacao-social/conselhos-e-orgaos-colegiados/conselho-nacional-de-previdencia-complementar/ementario-de-normas-do-conselho/resolucoes-cnpc/resolucao-no-41-de-2021.pdf. Acesso em: 12 set. 2022.

BRAVO, J. M. V. Tábuas de mortalidade contemporâneas e prospectivas: Modelos estocásticos, aplicações actuariais e cobertura do risco de longevidade. 2007. Tese (Doutorado em Economia) – Universidade de Évora, Évora, 2007. Disponível em: http://hdl.handle.net/10174/11148. Acesso em: 12 jul. 2022.

CARDOSO, S. A arquitetura dos Planos CD e CV: A forma de pagamento dos benefícios de aposentadoria programada. 2009. Monografia (Graduação em Ciências Atuariais) – Universidade Federal do Ceará, Fortaleza, 2009.

CARDOSO, S.; CHAGAS, D.; JÚNIOR, E.; ROCHA, A.; BATISTA, P. Pequenas e médias empresas como patrocinadoras de planos previdenciais em entidades fechadas de previdência complementar. Revista Contabilidade & Finanças, v. 17, p. 28-41, 2006.

CORRÊA, C. S. Tamanho populacional e aleatoriedade de eventos demográficos na solvência de RPPS municipais capitalizados. 2014. Tese (Doutorado em Demografia) – Centro de Desenvolvimento e Planejamento Regional da Faculdade de Ciências Econômicas, Universidade Federal de Minas Gerais, Belo Horizonte, 2014.

CORRÊA, C. S.; QUEIROZ, B. L.; RIBEIRO, A. J. F. Tamanho populacional e custeio previdenciário: como variações aleatórias afetam o risco de solvência de RPPS municipais. REDECA. Revista Eletrônica do Departamento de Ciências Contábeis & Departamentode Atuária e Métodos Quantitativos, 2014. Acesso em: 17 jul. 2022.

DIAS, C. R. B.; DOS SANTOS, J. Mensuração de passivo atuarial de fundos de pensão: Uma visão estocástica. In: CONGRESSO USP DE CONTROLADORIA E CONTABILIDADE, 2009. [S. l.: s. n.], 2009.

HÁRI, N; WAEGENAERE, A. D., MELENBERG, B.; NIJMAN, T. E. Longevity risk in portfolios of pension annuities, Insurance: Mathematics and Economics, Volume 42, Issue 2, 2008, Pages 505-519, ISSN 0167-6687, https://doi.org/10.1016/j.insmatheco.2007.01.012.

OLIVIERI, A.; PITACCO, E. Facing LTC Risks. In: PROCEEDINGS OF THE 32ND ASTIN COLLOQUIUM, 2001. Washington: [s. n.], 2001.

REILLY, F. L.; NORTON, E. A. Investimentos. 7. ed. São Paulo: Cengage Learning, 2008.

RIBEIRO, V. L.; CHARIGLIONE,I. P. F. S.; SALMAZO DA SILVA, H. Risco de Longevidade e Mecanismos de Proteção para Fundos de Pensão: Revisão Sistemática de Literatura. Revista Kairós-Gerontologia, 23(1), 415-449. ISSNprint 1516-2567. ISSNe 2176-901X.São Paulo (SP), Brasil: FACHS/NEPE/PUC-S, 2020.

ROCHA, A. S. Custos com benefícios para o financiamento de cuidados de longa duração para idosos com dependência: Estimativas e projeções para o Brasil. 2015. Tese (Douturado em Demografia) – Centro de Desenvolvimento e Planejamento Regional da Faculdade de Ciências Econômicas, Universidade Federal de Minas Gerais, Belo Horizonte, 2015.

RODRIGUES, J. A. Gestão de risco atuarial. São Paulo: Saraiva, 2008.

Recebido: 28/09/2023

Aceito: 30/09/2023